ODE Solvers, Process Error, and Difference Equations

The McMasterPandemic project has focused on using discrete time difference equations to solve the dynamical system. Here we describe experimental features that allow one to update the data differently. In particular, it is now possible to use a Runge-Kutta 4 ODE solver (to approximate the solution to the continuous time analogue) as well as the Euler Multinomial distribution to generate process error. These features have in principle been available for most of the life of macpan2, but only recently have they been given a more convenient interface.

In order to use this interface, models must be rewritten using explicit declarations of state updates. By explicitly declaring what expressions correspond to state updates, macpan2 is able to modify the method of updating without further user input. This makes it easier to compare difference equations (i.e. Euler steps), ODEs (i.e. Runge-Kutta), and process error (i.e. Euler Multinomial) runs for the same underlying dynamical model.

To declare a state update one replaces formulas in the during argument of a model spec to include calls to the mp_per_capita_flow() function. As an example we will modify the SI model to include explicit state updates. The original form of the model looks like this.

library(macpan2)
si_implicit = mp_tmb_model_spec(
    before = list(S ~ N - I)
  , during = list(
        infection ~ beta * S * I / N
      , S ~ S - infection
      , I ~ I + infection
    )
  , default = list(I = 1, N = 100, beta = 0.25)
)
print(si_implicit)
#> ---------------------
#> Default values:
#> ---------------------
#>  matrix row col  value
#>       I           1.00
#>       N         100.00
#>    beta           0.25
#> 
#> ---------------------
#> Before the simulation loop (t = 0):
#> ---------------------
#> 1: S ~ N - I
#> 
#> ---------------------
#> At every iteration of the simulation loop (t = 1 to T):
#> ---------------------
#> 1: infection ~ beta * S * I/N
#> 2: S ~ S - infection
#> 3: I ~ I + infection

The modified version looks like this.

si_explicit = mp_tmb_model_spec(
    before = list(S ~ N - I)
  , during = list(mp_per_capita_flow("S", "I", infection ~ beta * I / N))
  , default = list(I = 1, N = 100, beta = 0.25)
)
print(si_explicit)
#> ---------------------
#> Default values:
#> ---------------------
#>  matrix row col  value
#>       I           1.00
#>       N         100.00
#>    beta           0.25
#> 
#> ---------------------
#> Before the simulation loop (t = 0):
#> ---------------------
#> 1: S ~ N - I
#> 
#> ---------------------
#> At every iteration of the simulation loop (t = 1 to T):
#> ---------------------
#> 1: mp_per_capita_flow(from = "S", to = "I", rate = infection ~ beta * 
#>      I/N)

With this explicit spec we can make three different simulators.

si_euler = (si_explicit 
  |> mp_euler()
  |> mp_simulator(time_steps = 50, outputs = "infection")
)
si_rk4 = (si_explicit 
  |> mp_rk4()
  |> mp_simulator(time_steps = 50, outputs = "infection")
)
si_euler_multinomial = (si_explicit 
  |> mp_euler_multinomial()
  |> mp_simulator(time_steps = 50, outputs = "infection")
)

library(dplyr)
#> 
#> Attaching package: 'dplyr'
#> The following object is masked from 'package:macpan2':
#> 
#>     all_equal
#> The following objects are masked from 'package:stats':
#> 
#>     filter, lag
#> The following objects are masked from 'package:base':
#> 
#>     intersect, setdiff, setequal, union
trajectory_comparison = list(
    euler = mp_trajectory(si_euler)
  , rk4 = mp_trajectory(si_rk4)
  , euler_multinomial = mp_trajectory(si_euler_multinomial)
) |> bind_rows(.id = "update_method")
print(head(trajectory_comparison))
#>   update_method    matrix time row col     value
#> 1         euler infection    1   0   0 0.2475000
#> 2         euler infection    2   0   0 0.3079844
#> 3         euler infection    3   0   0 0.3828223
#> 4         euler infection    4   0   0 0.4751841
#> 5         euler infection    5   0   0 0.5888103
#> 6         euler infection    6   0   0 0.7280407

library(ggplot2)
(trajectory_comparison
  |> rename(`Time Step` = time, Incidence = value)
  |> ggplot()
  + geom_line(aes(`Time Step`, Incidence, colour = update_method))
)

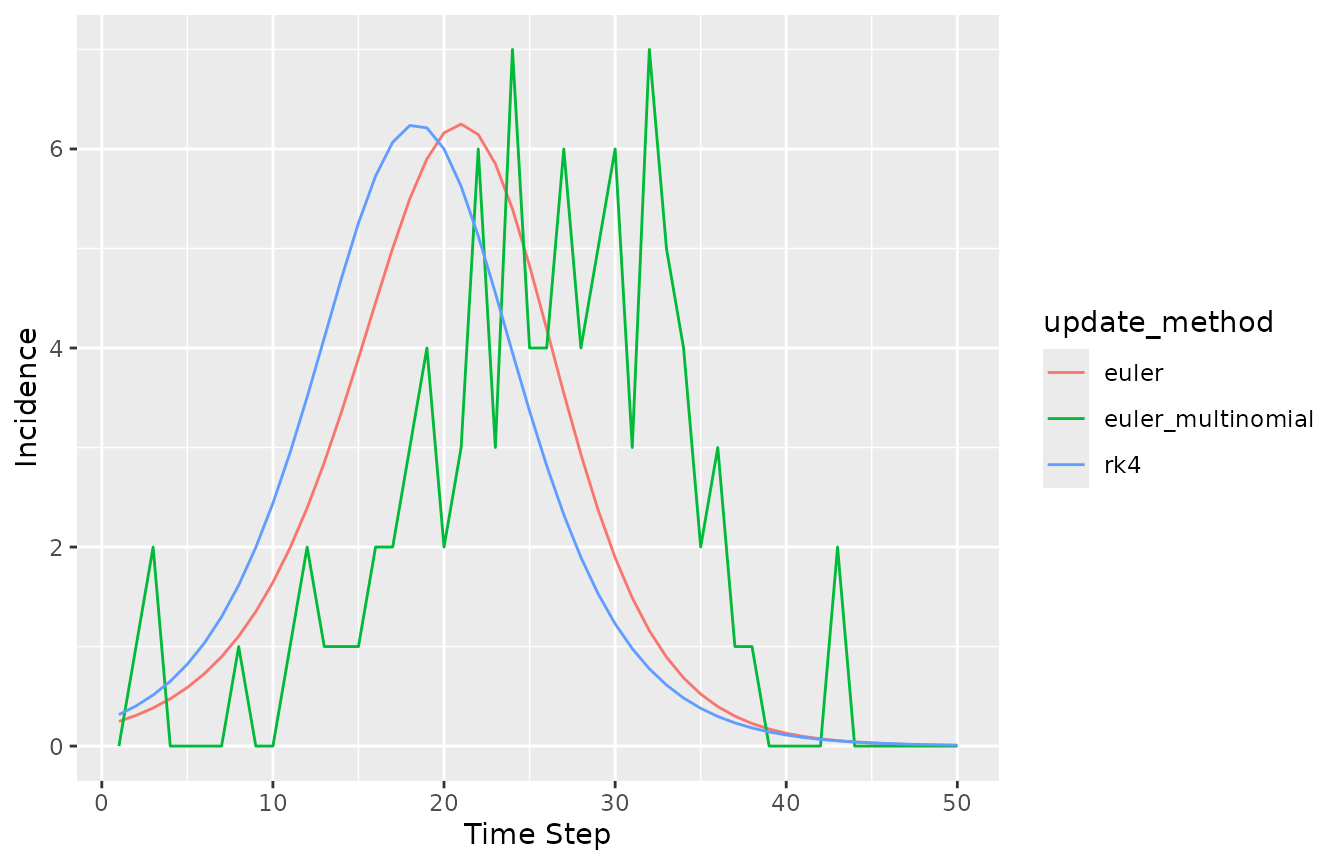
The incidence trajectory is different for the three update methods, even though the initial values of the state variables were identical in all three cases.

mp_initial(si_euler)
#>   matrix time row col  value
#> 1      N    0   0   0 100.00
#> 2      I    0   0   0   1.00
#> 3   beta    0   0   0   0.25
#> 4      S    0   0   0  99.00
mp_initial(si_euler_multinomial)
#>   matrix time row col  value
#> 1      N    0   0   0 100.00
#> 2      I    0   0   0   1.00
#> 3   beta    0   0   0   0.25
#> 4      S    0   0   0  99.00
mp_initial(si_rk4)
#>   matrix time row col  value
#> 1      N    0   0   0 100.00
#> 2      I    0   0   0   1.00
#> 3   beta    0   0   0   0.25
#> 4      S    0   0   0  99.00

The incidence is different, even during the first time step, because each state update method causes different numbers of susceptible individuals to become infectious at each time step. Further, incidence here is defined for a single time step and so this number of new infectious individuals is exactly the incidence.

Branching Flows and Process Error

 siv = mp_tmb_model_spec(
    before = list(S ~ N - I - V)
  , during = list(
        mp_per_capita_flow("S", "I", infection ~ beta * I / N)
      , mp_per_capita_flow("S", "V", vaccination ~ rho)
    )
  , default = list(I = 1, V = 0, N = 100, beta = 0.25, rho = 0.1)
)
print(siv)
#> ---------------------
#> Default values:
#> ---------------------
#>  matrix row col  value
#>       I           1.00
#>       V           0.00
#>       N         100.00
#>    beta           0.25
#>     rho           0.10
#> 
#> ---------------------
#> Before the simulation loop (t = 0):
#> ---------------------
#> 1: S ~ N - I - V
#> 
#> ---------------------
#> At every iteration of the simulation loop (t = 1 to T):
#> ---------------------
#> 1: mp_per_capita_flow(from = "S", to = "I", rate = infection ~ beta * 
#>      I/N)
#> 2: mp_per_capita_flow(from = "S", to = "V", rate = vaccination ~ 
#>      rho)

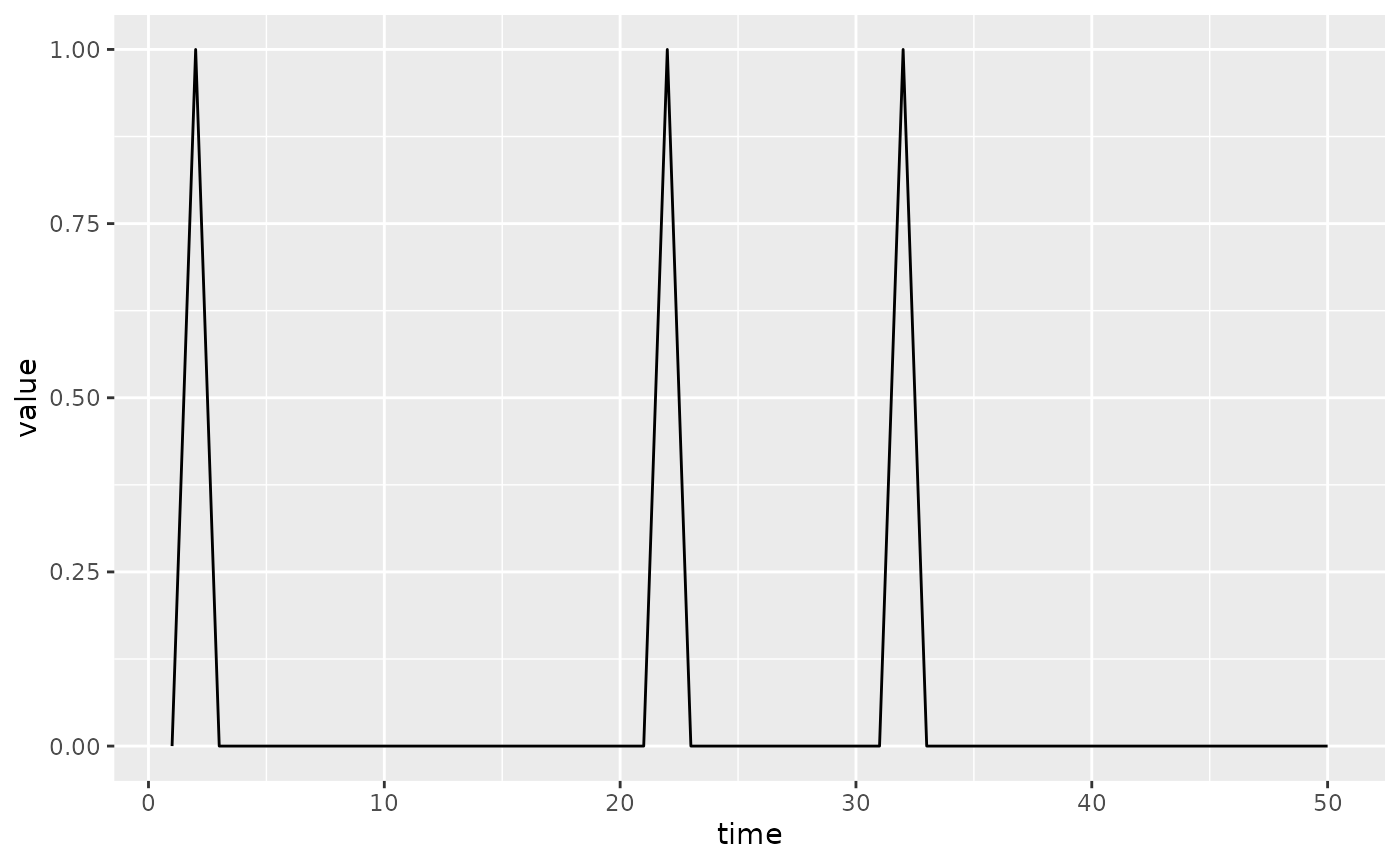
(siv 
 |> mp_euler_multinomial()
 |> mp_simulator(50, "infection")
 |> mp_trajectory()
 |> ggplot()
  + geom_line(aes(time, value))
)

Internal Design

sir = mp_tmb_model_spec(
  during = list(
      N ~ S + I + R
    , mp_per_capita_flow("S", "I", "beta * I / N", "infection")
    , mp_per_capita_flow("I", "R", "(1 - p) * gamma", "recovery")
    , mp_per_capita_flow("I", "D", "p * gamma", "death")
  )
)

`ChangeComponent()` classes

Model specs contain a set of three lists: * before : instructions to run before the simulation loop begins. * during : instructions to run at each iteration of the simulation loop. * after : instructions to run after the simulation loop ends.

The simplest way to define these lists is using two-sided R formulas. But in the during list one may specify different types of list components, which are of class ChangeComponent. Internally, standard R formulas are converted into an object of class Formula, which is the simplest kind of ChangeComponent. Another important ChangeComponent is the PerCapitaFlow type, which is used for standard flows from one compartment to another.

The list of change components, which is just the during field but ensuring that all elements are valid ChangeComponent objects, can be obtained using the change_components() method in a model spec object.

cc = sir$change_components()
print(cc)
#> [[1]]
#> N ~ S + I + R
#> 
#> [[2]]
#> From: S
#> To: I
#> Per-capita rate expression: beta * I/N
#> Absolute rate symbol: infection
#> [[3]]
#> From: I
#> To: R
#> Per-capita rate expression: (1 - p) * gamma
#> Absolute rate symbol: recovery
#> [[4]]
#> From: I
#> To: D
#> Per-capita rate expression: p * gamma
#> Absolute rate symbol: death

All ChangeComponent objects must have the following methods.

The `change_frame()` method

Returns a data frame with two columns: * state : state variable being changed (i.e. updated at each step) * change : signed absolute flow rates (variables or expressions that don’t involve any state variables)

An example of this data frame for a flow from S to I is as follows.

cc[[2]]$change_frame()
#>   state     change
#> 1     S -infection
#> 2     I +infection

For a simple Formula change component this data frame is just an empty two-column data frame with zero rows.

cc[[1]]$change_frame()
#> [1] state  change
#> <0 rows> (or 0-length row.names)

The `flow_frame()` method

Returns a data frame with three columns. * size : variable (often a state variable or function of state variables) that gives the size of the population being drawn from in a flow (e.g. S is the size of an infection flow). * change : unsigned absolute flow rates. * rate : per-capita flow rates (variables or expresions that sometimes involve state variables).

An example of this data frame for a flow from S to I is as follows.

cc[[2]]$flow_frame()
#>   size    change       rate         abs_rate
#> 1    S infection beta * I/N S * (beta * I/N)

For a simple Formula change component this data frame is just an empty three-column data frame with zero rows.

cc[[1]]$flow_frame()
#> [1] size     change   rate     abs_rate
#> <0 rows> (or 0-length row.names)

`ChangeModel()` classes

The ChangeModel objects combine the information in lists of ChangeComponent objects, so that they specify a full model. It expands the concept of before, during, and after into a more refined set of steps. All of these methods return lists of two-sided formulas.

before_loop() : The before list formulas.
once_start() : Formulas to evaluate at the start of the during list, and which will not be repeated (or modified and repeated) throughout expansions of the during loop. An example of such an expansion is a Runge-Kutta differential equation solver that reuses expressions in an iterative manner. Formulas returned by once_during() are useful for specifying exogeneous changes (e.g., time-varying parameters) that occur once per time-step but that should not change throughout the within-time-step iterations of a differential equation solver.
before_flows() : Formulas to evaluate before the absolute flow rates are computed.
update_flows() : Formulas that update the flows, using flow_frame() methods of individual ChangeComponent objects.
before_state() : Formulas to evaluate before the state vector is updated.
update_state() : Formulas that update the state vector, using change_frame() method s of individual ChangeComponent objects.
after_state() : Formulas to evaluate after the state vector is updated.
once_end() : Formulas to evaluate at the end of the during list, and which will not be repeated throughout (similar to once_start()).
after_loop() : The after list formulas.

The ChangeModel objects also have flow_frame() and change_frame() methods for combining the outputs of these methods within the individual ChangeComponent objects. An example for an SIR model gives the flow_frame() and change_frame() output as follows.

state   change
-----   ------
S       -infection
I       +infection
I       -recovery
R       +recovery

size  change     rate
----  ------     ----
S     infection  beta * I / N
I     recovery   gamma

The update_flows() method The update_state() method makes use of this flow_frame() to produce the

si = mp_tmb_library("starter_models", "sir", package = "macpan2")
si$change_model
#> Classes 'SimpleChangeModel', 'ChangeModelDefaults', 'ChangeModel', 'Base' <environment: 0x55a56aa1d908> 
#> after_loop : function ()  
#> after_state : function ()  
#> all_user_aware_names : function ()  
#> before_flows : function ()  
#> before_loop : function ()  
#> before_state : function ()  
#> change_classes : function ()  
#> change_frame : function ()  
#> flow_frame : function ()  
#> no_change_components : function ()  
#> once_finish : function ()  
#> once_start : function ()  
#> other_generated_formulas : function ()  
#> update_flows : function ()  
#> update_state : function ()  
#> user_formulas : function ()
si$change_model$flow_frame()
#>   size    change       rate         abs_rate
#> 1    S infection I * beta/N S * (I * beta/N)
#> 2    I  recovery      gamma      I * (gamma)
si$change_model$change_frame()
#>   state     change
#> 1     S -infection
#> 2     I +infection
#> 3     I  -recovery
#> 4     R  +recovery
si$change_model$update_state()
#> [[1]]
#> S ~ -infection
#> <environment: 0x55a56a1dde20>
#> 
#> [[2]]
#> I ~ +infection - recovery
#> <environment: 0x55a56a1dde20>
#> 
#> [[3]]
#> R ~ +recovery
#> <environment: 0x55a56a1dde20>
si$change_model$update_flows()
#> $S
#> $S[[1]]
#> infection ~ I * beta/N
#> <environment: 0x55a56a06efc0>
#> 
#> 
#> $I
#> $I[[1]]
#> recovery ~ gamma
#> <environment: 0x55a56a06efc0>

spec = mp_tmb_model_spec(
  during = list(
      mp_per_capita_flow("A", "B", "a", "r")
    , mp_per_capita_flow("B", "C", "b", "rr")
  )
)
spec$change_model$update_flows()
#> $A
#> $A[[1]]
#> r ~ a
#> <environment: 0x55a569956fc0>
#> 
#> 
#> $B
#> $B[[1]]
#> rr ~ b
#> <environment: 0x55a569956fc0>

`UpdateMethod()` classes

In order to define a state updater one must define a new UpdateMethod class. These classes are required to update three methods that do not take any arguments: before, during, and after. Each of these methods are required to return a list of two-sided formulas giving the expression list for the three phases of the simulation: before the simulation loop, at every iteration of the simulation loop, and after the simulation loop. Examples of UpdateMethod classes include: EulerUpdateMethod, RK4UpdateMethod, EulerMultinomialUpdateMethod, and HazardUpdateMethod.

The constructors of these UpdateMethod classes often have a field of class ChangeModel, which specifies how to sort the components of

Relationship to Ordinary Differential Equation Solvers

It is instructive to view these state update methods as approximate solutions to ordinary differential equations (ODEs). We consider ODEs of the following form.

$\frac{dx_i}{dt} = \underbrace{\sum_j x_j r_{ji}}_{\text{inflow}} - \underbrace{\sum_j x_i r_{ij}}_{\text{outflow}}$ Where the per-capita rate of flowing from compartment $i$ to compartment $j$ is $r_{ij}$ , and $x_i$ is the number of individuals in the $i$ th compartment. We allow each $r_{ij}$ to depend on any number of state variables and time-varying parameters. For example, for an SIR model we have $x_S, x_I, x_R$ (for readability we use $S, I, R$ ). In this case $r_{SI} = \beta I / N$ , $r_{IR} = \gamma$ , and all other values of $r_{ij}$ are zero. Here the force of infection, $r_{SI}$ , depends on a state variable $I$ .

Although each state-update method presented below can be thought of as an approximate solution to this ODE, they can also be thought of as dynamical models in their own right. For example, the Euler-multinomial model is a useful model of process error.

Euler

The simplest approach is to just pretend that the ODEs are difference equations. In this case, at each time-step, each state variable is updated as follows. $x_i = x_i - \sum_j x_i r_{ij} + \sum_j x_j r_{ji}$ The SIR example is as follows.

$S = S - Sr_{SI}$ $I = I - Ir_{IR} + Sr_{SI}$ $R = R + Ir_{IR}$

Runge Kutta 4

TODO

Euler-Multinomial

The Euler-multinomial state update method assumes that the number of individuals that move from one box to another in a single time-step is a random non-negative integer, coming from a particular multinomial distribution that we now describe.

The probability of staying in the $i$ th box through an entire time-step is assumed to be the following (TODO: relate this to Poisson processes).

$p_{ii} = \exp\left(-\sum_j r_{ij}\right)$

This probability assumes that the $r_{ij}$ are held constant throughout the entire time-step, although they can change when each time-step begins.

The probability of moving from box $i$ to box $j$ in one time-step is given by the following.

$p_{ij} = (1 - p_{ii}) \frac{r_{ij}}{\sum_j r_{ij}}$

This probability is just the probability of not staying in box $i$ , which is $1 - p_{ii}$ , and specifically going to box $j$ , which is assumed to be given by this expression $\frac{r_{ij}}{\sum_j r_{ij}}$ .

Let $\rho_{ij}$ be the random number of individuals that move from box $i$ to box $j$ in one time-step. The expected value of $\rho_{ij}$ is $p_{ij} x_i$ . However, these random variables are not independent events, because the total number of individuals, $\sum_i x_i$ , has to remain constant through a single time-step (at least in the models that we are currently considering).

To account for this non-independence, we collect the $\rho_{ij}$ associated with a from compartment $i$ into a vector $\rho_i$ . We collect similar vector of probabilities, $p_i$ . Each $\rho_i$ is a random draw from a multinomial distribution with $x_i$ trials and probability vector, $p_i$ .

Once these random draws have been made, the state variables can be updated at each time-step as follows.

$x_i = x_i - \sum_j \rho_{ij} + \sum_j \rho_{ji}$

Note that we do not actually need to generate values for the diagonal elements, $\rho_{ii}$ , because they cancel out in this update equation. We also can ignore any $\rho_{ij}$ such that $r_{ij} = 0$ .

Under the SIR example we have a particularly simple Euler-binomial distribution because there are no branching flows – when individuals leave S they can only go to I and when they leave I they can only go to R. These two flows are given by the following distributions.

$\rho_{SI} \sim \text{Binomial}(S, p_{SI})$

$\rho_{IR} \sim \text{Binomial}(I, p_{IR})$

In models with branching flows we would have multinomial distributions. But in this model the state update is given by the following equations.

$S = S - \rho_{SI}$ $I = I - \rho_{IR} + \rho_{SI}$ $R = R + \rho_{IR}$

Hazard

The Hazard update-method uses the expected values associated with the Euler-multinomial described above. In particular, the state variables are updated as follows.

$x_i = x_i - \sum_j x_i p_{ij} + \sum_j x_j p_{ji}$

The SIR model would be as follows.

$S = S - Sp_{SI}$ $I = I - Ip_{IR} + Sp_{SI}$ $R = R + Ip_{IR}$

More explicitly for the $I$ compartment this would be. $I(t+1) = I(t) - I(t) (1 - \exp(-\gamma)) + S(t)(1 - \exp(-\beta I(t)))$

Linearizing at Each Time-Step

Because the $r_{ij}$ could depend on any state variable, the ODE above is generally non-linear. However, we could linearize the model at every time-step and explicitly compute the matrix exponential to find the approximate state update.

Hazard in models including more than unbalanced per-capita flows

The perfectly balanced per-capita flows approach used above does not always work. For example, virus shedding to a wastewater compartment does not involve infected individuals flowing into a wastewater compartment, because people do not become wastewater obviously. In such models we need to think more clearly about how to use the Hazard approximation.

For such cases we can modify the differential equation to include an arbitrary number of absolute inflows and outflows.

$\frac{dx_i}{dt} = \underbrace{\sum_j x_j r_{ji}}_{\text{inflow}} - \underbrace{\sum_j x_i r_{ij}}_{\text{outflow}} + \underbrace{\sum_k r^+_{ik}}_{\text{absolute inflow}} - \underbrace{\sum_l r^-_{il}}_{\text{absolute outflow}}$

Where $r^+_{ik}$ is the absolute rate at which $x_i$ increases due to mechanism $k$ and $r^-_{il}$ is the absolute rate at which $x_i$ decreases due to mechanism $l$ .