Skip to contents

Advanced Specification of Time-Varying Parameters

Source: vignettes/time_varying_parameters_advanced.Rmd
time_varying_parameters_advanced.Rmd

status

Baseline SIR Model

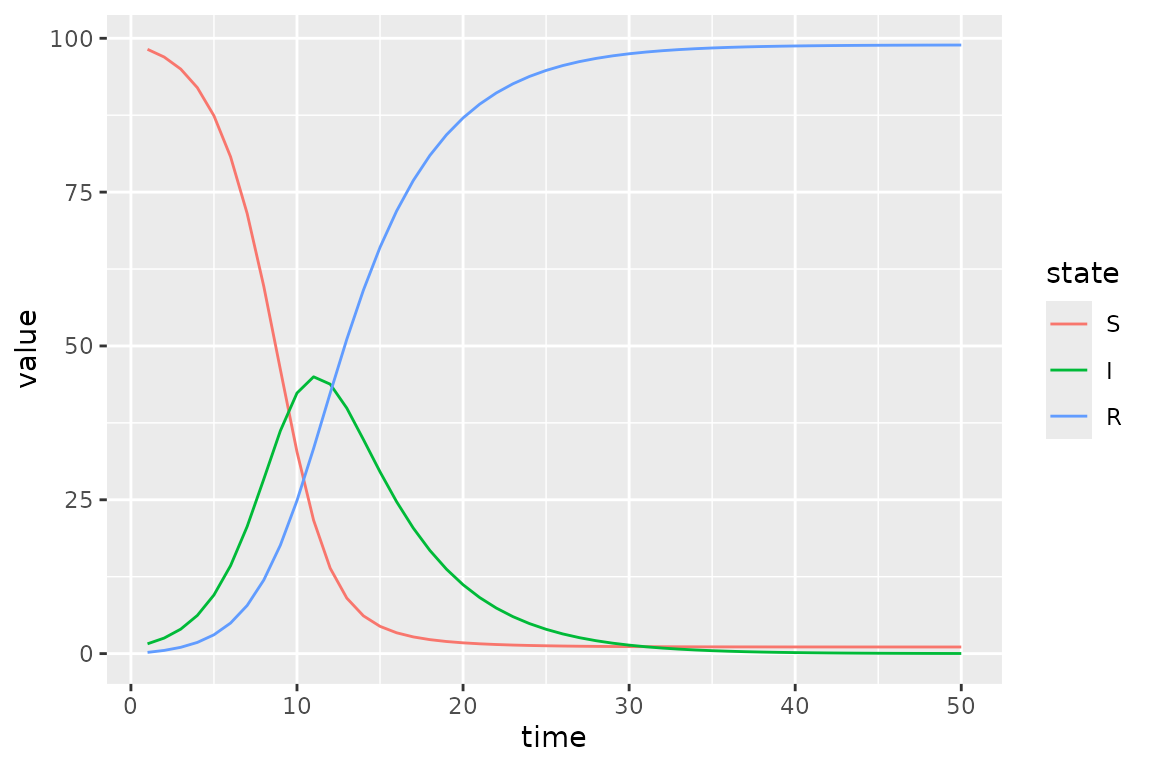
Here we modify an SIR model so that transmission rate is time-varying.

state_labels = c("S", "I", "R")
simulator = ("starter_models"
  |> mp_tmb_library("sir", package = "macpan2")
  |> mp_simulator(time_steps = 50
    , outputs = state_labels
    , default = list(beta = 0.8, gamma = 0.2)
  )
)
(simulator
  |> mp_trajectory()
  |> mutate(state = factor(matrix, state_labels))
  |> ggplot() 
  + geom_line(aes(time, value, colour = state))
)

Piecewise Time Variation

We now change the value of the transmission rate, beta, at the beginning of time-step 10 and 15. In the first step we add to the simulator a vector containing these change-points.

simulator$add$matrices(beta_changepoints = c(0, 10, 15))

Next we add the values to which beta changes at these time-steps.

simulator$add$matrices(beta_values = c(0.8, 0.01, 0.4))

We also need a variable to track the current value of beta. This beta_pointer starts at time-step equal to 0, and it will be incremented throughout the simulation.

simulator$add$matrices(beta_pointer = 0)

We increment beta_pointer using the time_group function that returns either beta_pointer or beta_pointer + 1 depending on whether or not the current time-step is at a change-point in beta_changepoints.

simulator$insert$expressions(
    beta_pointer ~ time_group(beta_pointer, beta_changepoints), 
    .phase = "during"
)

We update beta at every iteration of the simulation loop using this beta_pointer.

simulator$insert$expressions(
  beta ~ beta_values[beta_pointer],
  .phase = "during"
)

Now we plot the updated simulations using these change-points, which we highlight with vertical lines.

s = mp_trajectory(simulator)
cp = simulator$get$initial("beta_changepoints")
(s
  %>% mutate(state = factor(matrix, state_labels))
  %>% ggplot()
  + geom_line(aes(time, value, colour = state))
  + geom_vline(
    aes(xintercept = x), 
    linetype = "dashed", 
    alpha = 0.5, 
    data = data.frame(x = cp)
  )
)

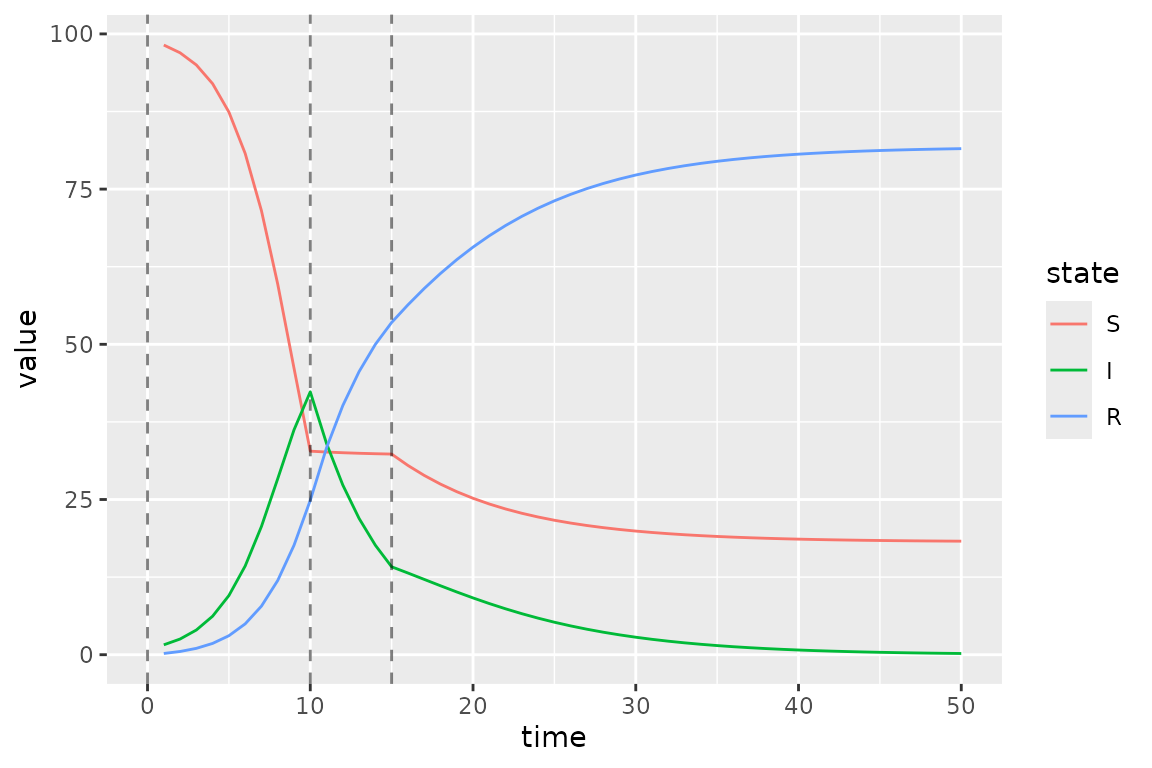
The clear kinks at times 10 and 15 are due the drop and then lift of the transmission rate at these times.

Calibrating Time Variation Parameters

First we simulate data to fit our model to, to see if we can recover the time-varying parameters.

set.seed(1L)
I_observed = rpois(50
  , filter(s, matrix == "I")$value
)
plot(I_observed)

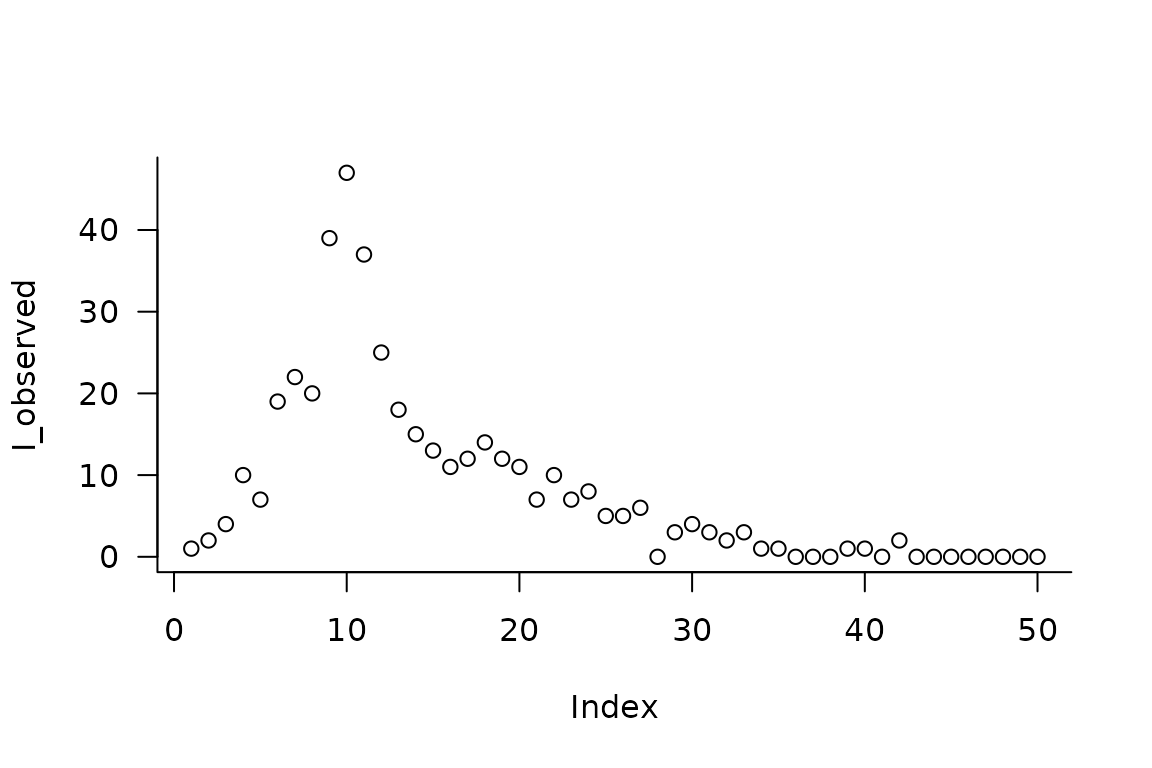
Then we add a few matrices to the model for keeping tracking of information used in model fitting.

simulator$update$matrices(
  
  ## observed data
  I_obs = I_observed,
  
  ## simulated trajectory to compare with data
  I_sim = empty_matrix, 
  
  ## location of I in the state vector
  ## (the `-1L` bit is to get 0-based indices instead of 1-based)
  I_index = match("I", state_labels) - 1L, 
  
  ## matrix to contain the log likelihood values at 
  ## each time step
  log_lik = empty_matrix, 
  
  ## need to save the simulation history of each of these matrices
  .mats_to_save = c("I_sim", "log_lik")
)

Now we need some new expressions. The first expression pulls out the I state from the state vector.

simulator$insert$expressions(
  I_sim ~ I,
  .phase = "during"
)

The second expression computes a vector of Poisson log-likelihood values – one for each time step.

simulator$insert$expressions(
  log_lik ~ dpois(I_obs, clamp(rbind_time(I_sim))),
  .phase = "after"
)
simulator$replace$obj_fn(~ -sum(log_lik))

Next we declare the beta values as parameters to be optimized on the log scale. The clearest way to do this is to form a data frame with one row for each parameter to be fitted.

default_beta = mean(simulator$get$initial("beta_values"))
params_to_fit = data.frame(
    mat = "log_beta_values"
  , row = 0:2
  , default = log(default_beta)
)
print(params_to_fit)
#>               mat row    default
#> 1 log_beta_values   0 -0.9079919
#> 2 log_beta_values   1 -0.9079919
#> 3 log_beta_values   2 -0.9079919

There are a couple potentially confusing aspects to this data frame. First, we want to fit the beta values on the log scale, and we indicate this by prepending log_ in front of the name of the beta_values matrix that is in the model. We will more explicitly add the log_beta_values matrix to the model in the next code chunk. Second, the word row corresponds to an index for the change points. In particular, row = 0 corresponds to the initial beta, row = 1 to the first change point and row = 2 to the second. This is because all quantities passed to macpan2 engines are matrices, and so in this case different rows of this log_beta_values matrix (actually column vector) correspond to different change points. If we were dealing with matrices with more than one column we would need to include a col column in this data frame to indicate the matrix columns of the matrix entries that correspond to parameters to be fitted.

Now we log transform the beta_values matrix entries and declare them as parameters.

simulator$add$transformations(Log("beta_values"))
simulator$replace$params_frame(params_to_fit)

Finally we fit the model back to the simulation data.

simulator$optimize$nlminb()
#> outer mgc:  736.1414 
#> outer mgc:  112.6655 
#> outer mgc:  71.38648 
#> outer mgc:  13.6616 
#> outer mgc:  12.58091 
#> outer mgc:  3.638083 
#> outer mgc:  1.399513 
#> outer mgc:  1.609453 
#> outer mgc:  1.140347 
#> outer mgc:  0.5870909 
#> outer mgc:  0.2527136 
#> outer mgc:  0.09938628 
#> outer mgc:  0.03753935 
#> outer mgc:  0.01394885 
#> outer mgc:  0.005150654 
#> outer mgc:  0.001897432 
#> outer mgc:  0.0006983805 
#> outer mgc:  0.0002569678 
#> outer mgc:  9.453968e-05 
#> outer mgc:  3.478009e-05 
#> outer mgc:  1.2795e-05 
#> outer mgc:  4.707033e-06 
#> outer mgc:  1.731623e-06 
#> outer mgc:  6.370285e-07 
#> outer mgc:  2.343501e-07 
#> outer mgc:  8.621238e-08 
#> outer mgc:  3.171574e-08
#> $par
#>      params      params      params 
#>  -0.1710158 -22.8268369  -0.8291142 
#> 
#> $objective
#> [1] 99.74231
#> 
#> $convergence
#> [1] 0
#> 
#> $iterations
#> [1] 26
#> 
#> $evaluations
#> function gradient 
#>       28       27 
#> 
#> $message
#> [1] "relative convergence (4)"

We can see that the optimizer converges (i.e. $convergence = 0) in 26 iterations.

On the log scale we see that the optimizer finds different values (current) than it started at (default).

simulator$current$params_frame()
#>   par_id             mat row col    default     current
#> 1      0 log_beta_values   0   0 -0.9079919  -0.1710158
#> 2      1 log_beta_values   1   0 -0.9079919 -22.8268369
#> 3      2 log_beta_values   2   0 -0.9079919  -0.8291142

More importantly the beta values on the untransformed scale recover reasonable values that are qualitatively consistent with the values used in the simulations.

data.frame(
  fitted = formatC(
    exp(simulator$current$params_frame()$current),
    format = "e", digits = 2
  ),
  true = simulator$get$initial("beta_values")
)
#>     fitted true
#> 1 8.43e-01 0.80
#> 2 1.22e-10 0.01
#> 3 4.36e-01 0.40

Note however that the second fitted beta value is much smaller than the true value, which is potentially interesting.

Radial Basis Functions for Flexible Time Variation (In-Progress)

This section uses radial basis functions (RBFs) to generate models with a flexible functional form for smooth changes in the transmission rate.

Before we can add the fancy radial basis for the transmission rate, we need a base model. We use an SIR model that has been modified to include waning.

sir = mp_tmb_library("starter_models"
  , "sir_waning"
  , package = "macpan2"
)

The macpan2::rbf function can be used to produce a matrix giving the values of each basis function (each column) at each time step (each row). Using this matrix, XX, and a weights vector, bb, we can get a flexible output vector, yy, with a shape that can be modified by changing the weights vector.

y=Xb y = Xb

The following code illustrates this approach.

set.seed(1L)
d = 20
n = 2500
X = rbf(n, d)
b = rnorm(d, sd = 0.01)
par(mfrow = c(3, 1)
  , mar = c(0.5, 4, 1, 1) + 0.1
)
matplot(X
  , type = "l", lty = 1, col = 1
  , ylab = "basis functions"
  , axes = FALSE
)
axis(side = 2)
box()
barplot(b
  , xlab = ""
  , ylab = "weights"
)
par(mar = c(5, 4, 1, 1) + 0.1)
plot(X %*% b
  , type = "l"
  , xlab = "time"
  , ylab = "output"
)

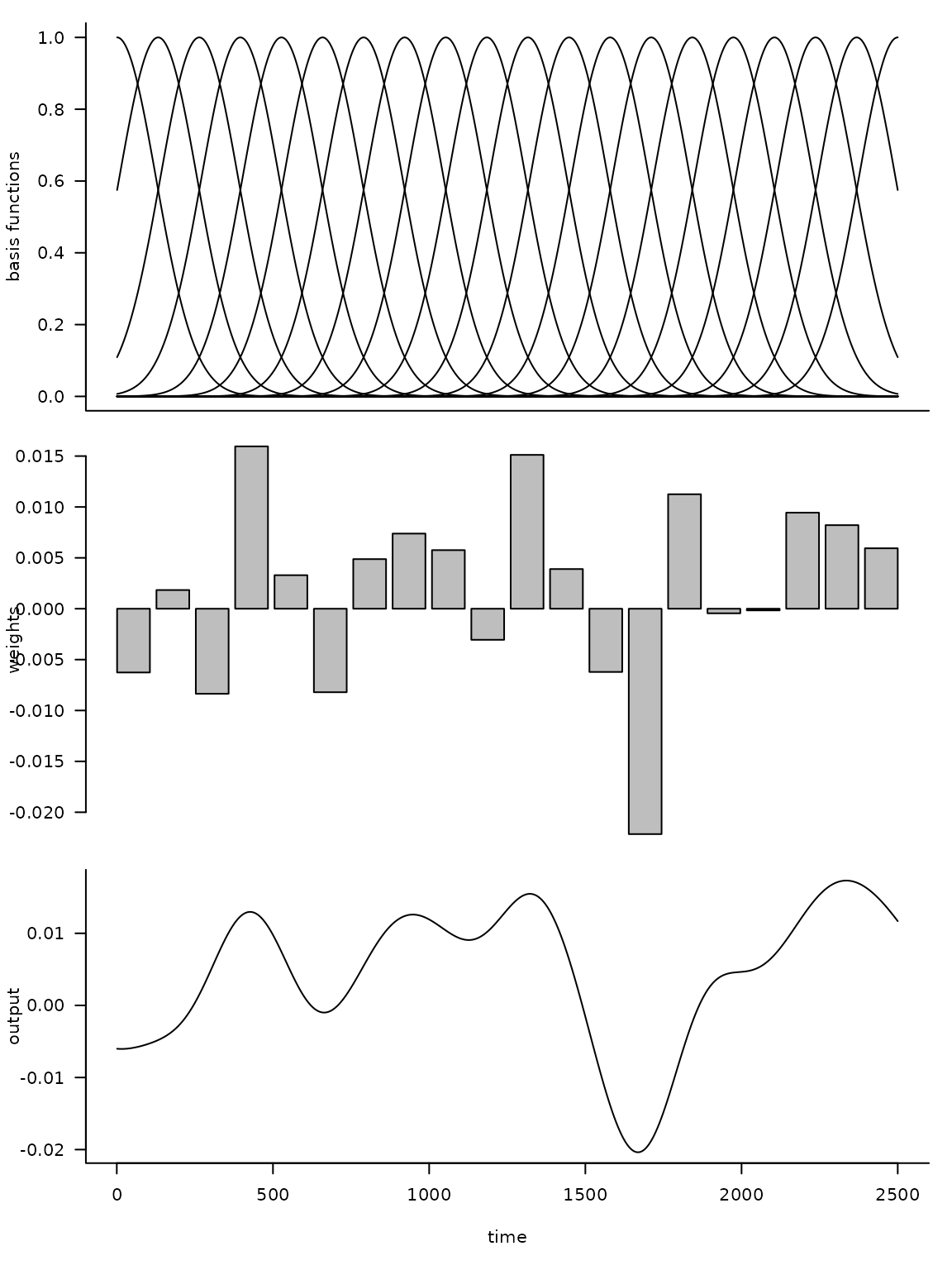
Here d is the dimension of the basis, or number of functions, and n is the number of time steps. By multiplying the uniform basis matrix (top panel) by a set of weights (middle panel), we obtain a non-uniform curve (bottom panel). Note how the peaks (troughs) in the output are associated with large positive (negative) weights.

Now we want to transform the output of the (matrix) product of the RBF matrix and the weights vector into a time-series for the transmission rate, β\beta. Although we could just use the output vector as the β\beta time series, it is more convenient to transform it so that the β\beta values yield more interesting dynamics in an SIR model. In particular, our model for βt\beta_t as a function of time, tt, is

log(βt)=log(γt)+log(N)−log(St)+xtb \log(\beta_t) = \log(\gamma_t) + \log(N) - \log(S_t) + x_tb

Here we have the recovery rate, γt\gamma_t, and number of susceptibles, StS_t, at time, tt, the total population, NN, and the ttth row of XX, xtx_t. To better understand the rationale for this equation note that if every element of bb is set to zero, we have the following condition.

βtStN=γt \frac{\beta_t S_t}{N} = \gamma_t

This condition assures that the number of infected individuals remains constant at time, tt. This means that positive values of bb will tend to generate outbreaks and negative values will tend to reduce transmission.

fixme: I (BMB) understand why you’re setting the model up this way, but it’s an odd/non-standard setup - may confuse people who are already familiar with epidemic models (it confused me initially).

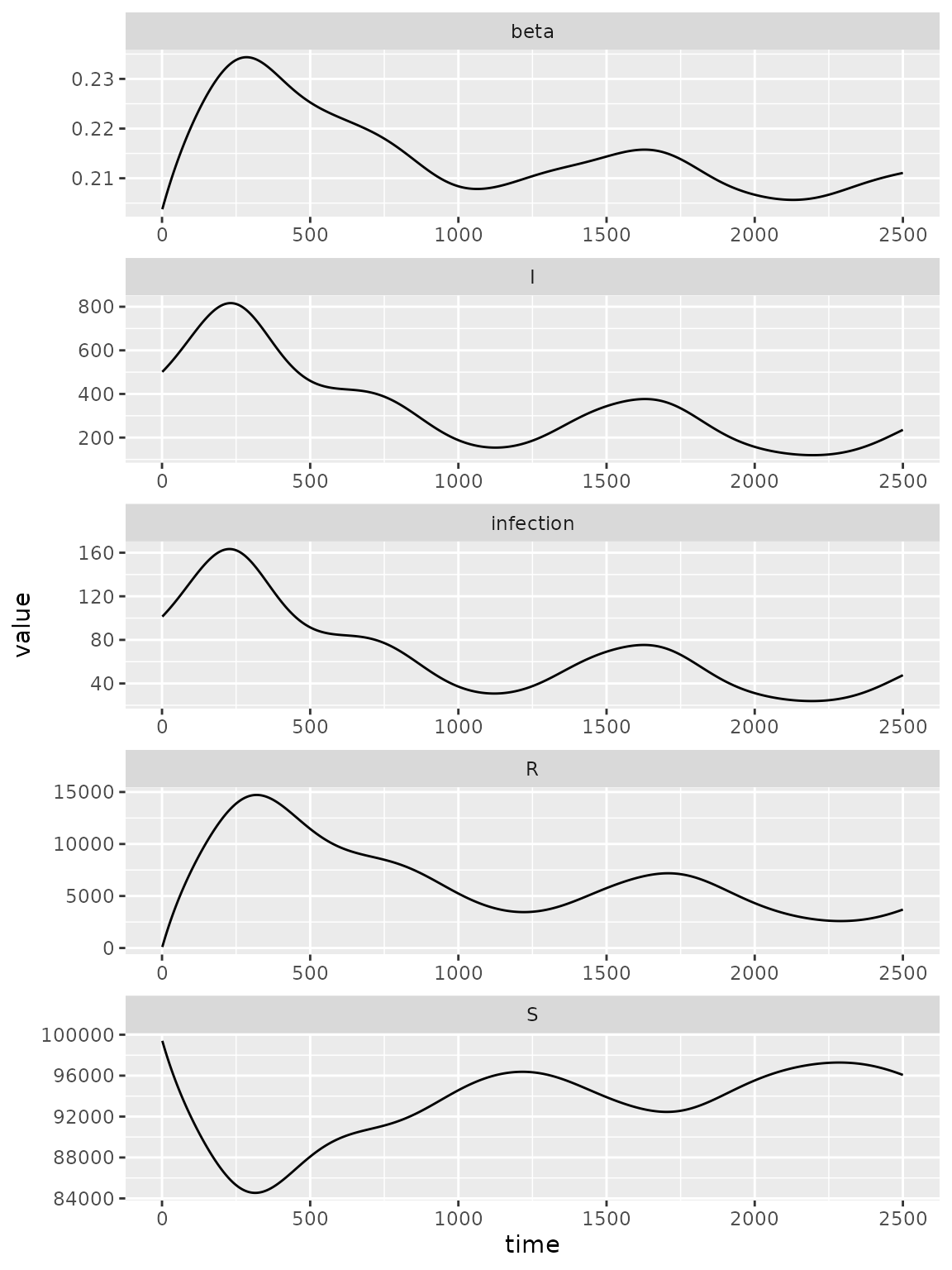
Here is a simulation model with a radial basis for exogenous transmission rate dynamics.

set.seed(1L)
simulator = mp_simulator(sir
  , time_steps = n
  , outputs = c("S", "I", "R", "infection", "beta")
  , default = list(
      N = 100000, I = 500, R = 0
    , beta = 1, gamma = 0.2, phi = 0.01
    , X = rbf(n, d)
    , b = rnorm(d, sd = 0.01)
  )
)
simulator$insert$expressions(
    eta ~ gamma * exp(X %*% b)
  , .phase = "before"
  , .at = Inf
)
simulator$insert$expressions(
    beta ~ eta[time_step(1)] / clamp(S/N, 1/100)
  , .phase = "during"
  , .at = 1
)
simulator$add$matrices(
    eta = empty_matrix
)
simulator$replace$params(
    default = rnorm(d, sd = 0.01)
  , mat = rep("b", d)
  , row = seq_len(d) - 1L
)
print(simulator)
#> ---------------------
#> Before the simulation loop (t = 0):
#> ---------------------
#> 1: S ~ N - I - R
#> 2: eta ~ gamma * exp(X %*% b)
#> 
#> ---------------------
#> At every iteration of the simulation loop (t = 1 to 2500):
#> ---------------------
#> 1: beta ~ eta[time_step(1)]/clamp(S/N, 1/100)
#> 2: infection ~ S * (I * beta/N)
#> 3: recovery ~ I * (gamma)
#> 4: waning_immunity ~ R * (phi)
#> 5: S ~ S - infection + waning_immunity
#> 6: I ~ I + infection - recovery
#> 7: R ~ R + recovery - waning_immunity
(simulator
 |> mp_trajectory()
 |> ggplot()
 + facet_wrap(~ matrix, ncol = 1, scales = 'free')
 + geom_line(aes(time, value))
)

Calibration

Now we’re going to calibrate this model to data. The main innovation here is that we will use a built-in feature of TMB (on which macpan2 is constructed), estimation of latent variables by Laplace approximation to fit the time series efficiently without overfitting (see section 5.10 of Madsen and Thyregod (2011), Kristensen et al. (2016), or the TMB documentation for more detail).

The next few steps will roughly follow the first example in the Calibration vignette: TODO: make sure to line this state up with the specific code in the calibration vignette.

1. Simulate from the model and add some noise:

obs_I <- (simulator
    |> mp_trajectory()
    |> filter(matrix == "I")
    |> mutate(across(value, ~ rnorm(n(), ., sd = 50)))
    |> pull(value)
)
plot(obs_I, xlab = "time", ylab = "prevalence")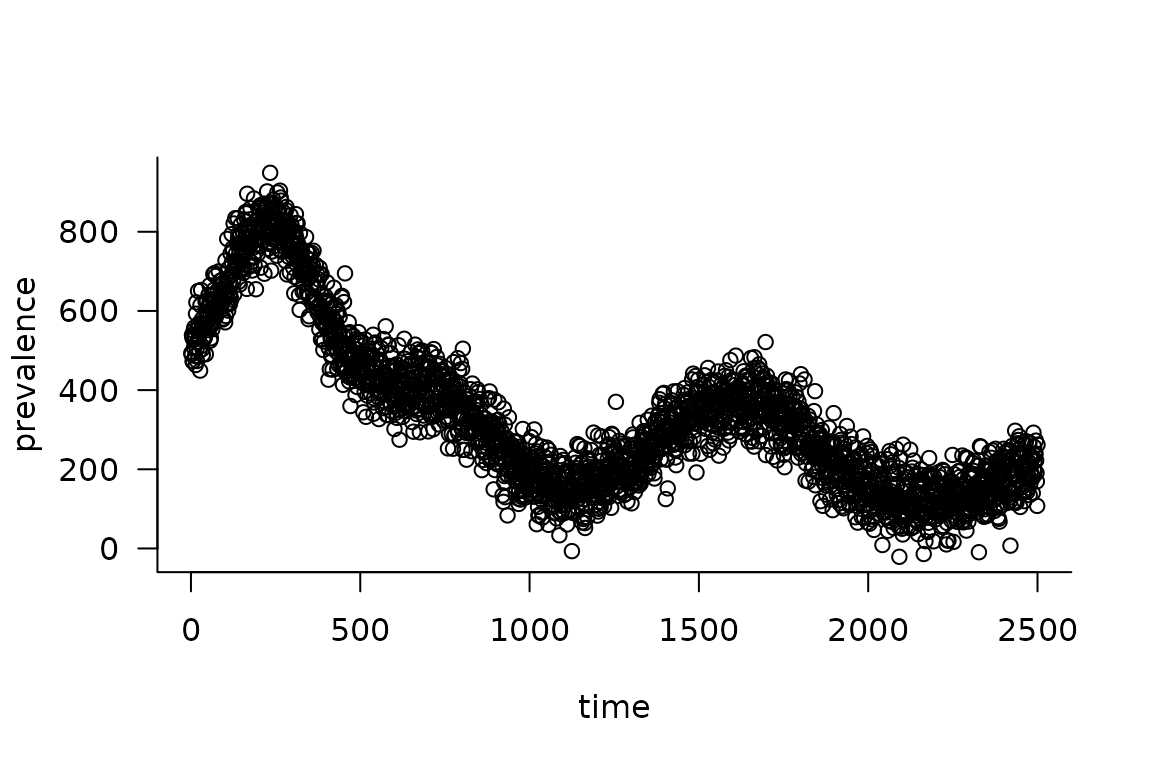

2. Add calibration information.

We start by adding standard boilerplate stuff to include the observed data and store/return the results.

## copied from 'calibration/"hello world"' example
simulator$add$matrices(
    I_obs = obs_I
  , I_sim = empty_matrix
  , log_lik = empty_matrix
  , .mats_to_save = c("I_sim")
  , .mats_to_return = c("I_sim")
)
simulator$insert$expressions(
     I_sim ~ I
   , .phase = "during"
   , .at = Inf
)

Now we start to deviate from the previous example: in addition to a parameter (I_sd) for the standard deviation of the noise in II, we also add a parameter (rbf_sd) for the variance of the RBF coefficients, and penalize the likelihood using

Iobs∼Normal(Isim(ϕ,𝐛),σI2)bi∼Normal(0,σrbf2) \begin{split} I_{\textrm{obs}} & \sim \textrm{Normal}(I_\textrm{sim}(\phi, {\mathbf b}), \sigma^2_I) \\ b_i & \sim \textrm{Normal}(0, \sigma^2_{\textrm{rbf}}) \end{split} and the likelihood is defined as: $$ \int {\cal L}(I_{\textrm{obs}}|\phi, {\mathbf b}', \sigma^2_I) \cdot {\cal L}({\mathbf b}'|\sigma^2_{\textrm{rbf}}) \, d{\mathbf b}. $$

The ϕ\phi vector is a set of fixed-effect (unpenalized) parameters; in this case it is empty, but it could include (for example) time-constant recovery or immune-waning rates, or a baseline transmission rate (see note below). (The fixed-effect parameter is usually denoted as β\beta in statistical models, but we’ve already used that symbol for the transmission coefficient …)

Although this looks awful, (1) the high-dimensional integral over 𝐛\mathbf b can be separated into a product of one-dimensional integrals and (2) the Laplace approximation gives us a quick, reasonable approximation to the one-dimensional integrals.

The rbf_sd parameter can be interpreted as a standard deviation on a Gaussian random effect or as approximately 1/λ1/\sqrt{\lambda} where λ\lambda is a ridge penalty.

Continuing with the coding, we add the parameters and negative log-likelihood to the model, making the negative log-likelihood a sum of the two terms in the integral above: the NLL of the data (-sum(dnorm(I_obs, ...))) and the likelihood of the RBF parameters (-sum(dnorm(b, ...))): we fit both of the SD parameters on the log scale.

simulator$add$matrices(
    I_sd = 1
  , rbf_sd = 1
)
simulator$insert$expressions(
     log_lik ~ 
       -sum(dnorm(I_obs, rbind_time(I_sim), I_sd)) +
       -1*sum(dnorm(b, 0.0, rbf_sd)),
     .phase = "after"
)
## initially forgot this: maybe we could warn when someone is missing this????
simulator$replace$obj_fn(~ log_lik)
simulator$add$transformations(Log("I_sd"))
simulator$add$transformations(Log("rbf_sd"))
## not sure if this is required?
params <- read.delim(sep = "|", header = TRUE,
                     strip.white = TRUE, ## important!
                      text = "
mat         | default
log_I_sd    | 0
log_rbf_sd  | 1
")
simulator$replace$params_frame(params)

Finally, we add the b vector as a set of random parameters: this tells macpan2 to apply the Laplace approximation to these parameters …

matrix_version = "1.6-5"
if (packageVersion("Matrix") >= matrix_version) {
  rparams <- data.frame(
      mat  = "b",
      row = 0:19,
      col = 0,
      default = 0)
  simulator$replace$random_frame(rparams)
}

Test the objective function:

if (packageVersion("Matrix") >= matrix_version) {
  res <- simulator$ad_fun()$fn(c(1,1))
}
#> iter: 1  value: 5994496 mgc: 2058657968 ustep: 1 
#> iter: 2  value: 1327494 mgc: 1334286157 ustep: 1 
#> iter: 3  value: 539106 mgc: 359174176 ustep: 1 
#> iter: 4  value: 461675.4 mgc: 72820581 ustep: 1 
#> iter: 5  value: 458020.4 mgc: 9231141 ustep: 1 
#> iter: 6  value: 457980.9 mgc: 605743.9 ustep: 1 
#> iter: 7  value: 457980.9 mgc: 7692.96 ustep: 1 
#> iter: 8  value: 457980.9 mgc: 2.548908 ustep: 1 
#> iter: 9  value: 457980.9 mgc: 1.89712e-06 ustep: 1 
#> mgc: 8.929342e-07
#> [1] 458152.8
#> attr(,"logarithm")
#> [1] TRUE

fixme: can’t get objective function to shut up. Should have specified silent = TRUE when calling MakeADFun() initially, now have tried assigning the value in several different environments, without success …

This step normally produces lots of output (more output than a model with random effects) because the Laplace approximation involves an additional “inner” step where the b parameters are optimized, even though we are only evaluating the objective for a single set of fixed parameters (log_I_sd, log_rbf_sd)

fixme: note to developers, if we cache results we may need to call the $retape() function to restore internal structure when retrieving …

if (packageVersion("Matrix") >= matrix_version) {
  ## testing: simulator$ad_fun()$fn()
  fit <- simulator$optimize$nlminb()
}
if (packageVersion("Matrix") >= matrix_version) {

  ## simulator$print$matrix_dims()
  ## fixed effects only:
  ## look at parameters, but skip the random-effects parameters
  ## 'random' holds the indices of the parameters that are treated
  ## as random effects
  (fixed_params <- with(simulator$ad_fun()$env,
                        last.par.best[-random]))
  ## ???
  ## RE only
  (ran_params <- with(simulator$ad_fun()$env,
                      last.par.best[random]))
}
#>        random        random        random        random        random 
#>  0.0067466350  0.0116662413 -0.0036351505 -0.0151989880  0.0011403827 
#>        random        random        random        random        random 
#>  0.0032615158 -0.0028962068 -0.0146686471 -0.0058110019  0.0073568463 
#>        random        random        random        random        random 
#>  0.0097221102  0.0023726453  0.0007574901  0.0014761570 -0.0134865091 
#>        random        random        random        random        random 
#> -0.0068787221 -0.0025147741  0.0027382985  0.0086679247  0.0033013692

fixme: we need an incantation to extract the full parameters (including RE parameters) in order to make sure $report works properly? (In general, should caution about mutability/make sure we use last.par.best internally …)

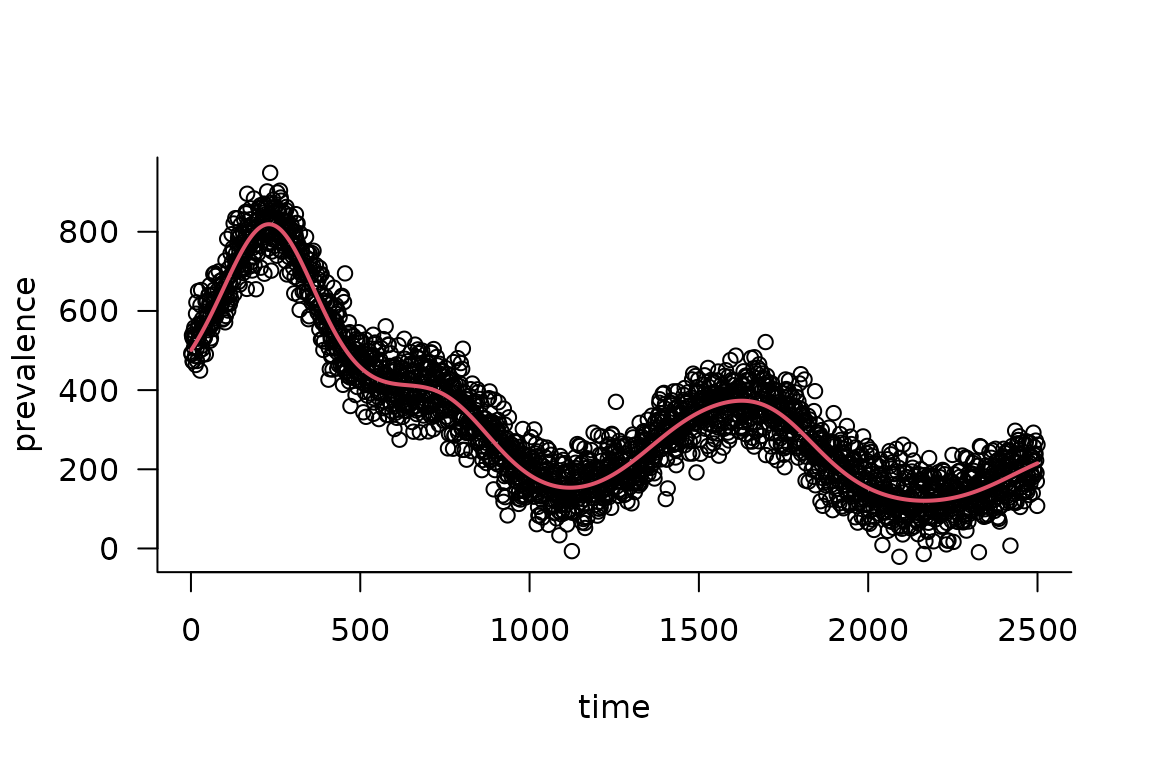
Extract parameters, run the simulator for the best-fit parameters, compare with data …

if (packageVersion("Matrix") >= matrix_version) {
  pp <- simulator$ad_fun()$env$last.par.best  ## FIXME: use this
  est_I <- (simulator
      |> mp_trajectory()
      |> filter(matrix == "I")
      |> pull(value)
  )
  par(las = 1, bty = "l")
  plot(obs_I, xlab = "time", ylab = "prevalence")
  lines(est_I, col = 2, lwd = 2)
}

fixme: there are a few artificialities about this example that could/should be relaxed

  • the only fixed parameters are the standard deviations. Normally we would also be estimating gamma (possibly with a prior? do we have any examples, say in the calibration vignette, of adding priors?)
  • the RBF function is penalized to zero. In general, we should augment the penalized RBF component (which determines the variation around the mean) with an unpenalized intercept/baseline transmission parameter. So, for example, the transmission rate should be computed as b0 + exp(X %*% b), where b0 represents an unpenalized parameter that’s allowed to vary freely …

fixme: compare (1) unpenalized fit; (2) penalized fit without Laplace approximation …

fixme: discuss (somewhere) alternate bases for latent variables (random-walk, Gaussian process, …)

References

Kristensen, Kasper, Anders Nielsen, Casper W. Berg, Hans Skaug, and Bradley M. Bell. 2016. “TMB: Automatic Differentiation and Laplace Approximation.” Journal of Statistical Software 70 (5). https://doi.org/10.18637/jss.v070.i05.
Madsen, Henrik, and Poul Thyregod. 2011. Introduction to General and Generalized Linear Models. CRC Press.